반응형
이진탐색이란?
배열의 중앙에 있는 값을 알아내어 찾고자 하는 항목이 중앙의 왼쪽에 있는지 오른쪽에 있는지를 알아내어 탐색의 범위를 반으로 줄이는 방법
단, 배열이 반드시 정렬이 되어있어야하기 때문에 고정된 데이터에 적합하다.
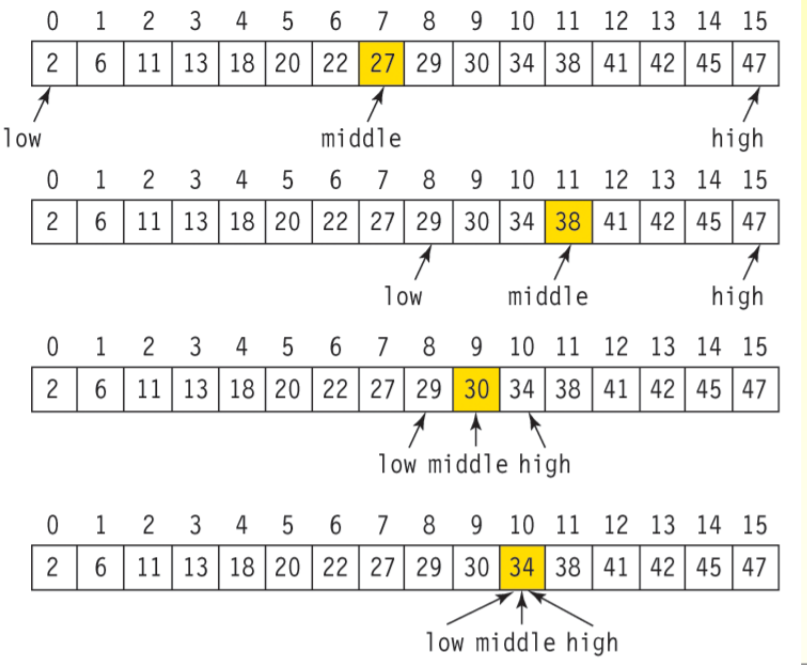
위의 예시는 34를 찾는 경우이다.
1. 34는 중앙값인 27보다 크므로 오른쪽 부분에서 탐색한다.
2. 다시 오른쪽 부분의 중앙값인 38과 비교한다. 38보다 작으므로 왼쪽 부분에서 탐색한다.
3. 다시 왼쪽 부분의 중앙값인 30과 비교한다. 30보다 크므로 오른쪽 부분에서 탐색한다.
4. 다시 오른쪽 부분의 중앙값인 34과 비교한다. 찾고자 하는 값이 중앙값과 일치한다.
즉, 중앙값과 비교하면서 찾고자하는 항목이 중앙값보다 작으면 왼쪽에서 다시 중앙값과 비교하고, 크면 오른쪽에서 다시 중앙값과 비교하는 과정을 반복하면서 항목을 탐색한다.
반복을 사용한 코드
#include <stdio.h>
int list[9] = { 1, 3, 5, 6, 7, 9, 11, 20, 30 };
int search_binary(int key, int low, int high) {
int middle;
while (low <= high) { //low와 high가 같을때까지만 반복
middle = (low + high) / 2;
if (key == list[middle])
return middle; //찾고자하는 항목이 중앙값과 일치하면 중앙값을 반환
else if (key < list[middle])
high = middle - 1; //찾고자하는 항목이 중앙값보다 작으면 왼쪽에서 탐색
else
low = middle + 1; //찾고자하는 항목이 중앙값보다 크면 오른쪽에서 탐색
}
return -1; //탐색 실패시 -1 반환
}
int main(void) {
int num = search_binary(1, 0, 8);
printf("%d", num);
}
순환(재귀)을 사용한 코드
#include <stdio.h>
int list[9] = { 1, 3, 5, 6, 7, 9, 11, 20, 30 };
int search_binary(int key, int low, int high) {
int middle;
if (low <= high) {
middle = (low + high) / 2;
if (key == list[middle])
return middle; //찾고자하는 항목이 중앙값과 일치하면 중앙값 반환
else if (key < list[middle])
return search_binary(key, low, middle - 1); //찾고자하는 항목이 중앙값보다 작으면 왼쪽에서 탐색
else
return search_binary(key, middle + 1, high); //찾고자하는 항목이 중앙값보다 크면 오른쪽에서 탐색
}
return -1; //탐색 실패시 -1 반환
}
시간복잡도
탐색 횟수가 0, 1, 2 ... 로 늘어날수록 탐색 범위는 n, n/2, n/4... 이렇게 절반으로 줄어든다. 탐색 범위를 더 이상 줄일 수 없는 1이 될 때의 탐색 횟수를 k라고 하면, 탐색 범위는 n/2^k가 된다.
$$k={log}_{2}n$$이 되고, 시간 복잡도는 $$O({log}_{2}n)$$ 가 된다.
반응형
'⚙️ 알고리즘 > 개념 정리' 카테고리의 다른 글
| [알고리즘/C] 삽입정렬(insertion sort) (0) | 2020.07.30 |
|---|---|
| [알고리즘/C] 버블 정렬(bubble sort) (0) | 2020.07.30 |
| [알고리즘] 순환(recursion) (0) | 2020.07.22 |
| [알고리즘] 알고리즘 효율성 - 최선, 평균, 최악의 경우 (0) | 2020.07.22 |
| [알고리즘] 공간 복잡도, 시간 복잡도, 빅오 표기법 (0) | 2020.07.22 |